Система "Хищник-жертва"
Рассмотрим примеры применения указанной модели для изучения взаимоотношений в системе «хищник — жертва». На рисунке 9 приведен пример колебательного режима по численности хищника и жертвы во времени. Можно видеть, что первоначальный подъем числа зайцев сопровождается выраженным увеличением числа лисиц. Это естественно, так как рост числа зайцев приводит к увеличению количества пищи для лисиц, что увеличивает скорость их размножения. Однако активное поедание зайцев лисами приводит в дальнейшем к падению численности жертвы. В свою очередь, это приводит к последующему снижению численности хищника. С другой стороны, снижение численности хищника приводит к повышению численности жертвы и последующему росту числа хищника.
 |
Рис. 1. Колебательный режим в системе «хищник — жертва» (хищник — лисы(красная линия), жертва — зайцы, (синяя линия)) |
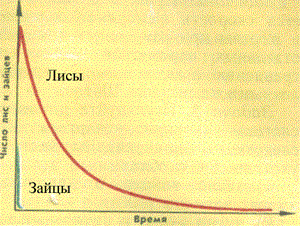 |
Рис. 2. Нежим вымирания в системе «хищник — жертва» начальное число зайцев Х0=100; начальное число лис Yo=200; коэффициент размножения зайцев Y1 = 2; коэффициент истребления зайцев y1—0,5; коэффициент ресурсный для зайцев m1 = 0,01; коэффициент размножения лис Y2=0,2; коэффициент смертности лис y2=0,4; коэффициент ресурсный для лис m2=0,001; время счета Т=10; |
Такова природа колебаний численности хищника и жертвы, которые наблюдаются
в указанной экосистеме. Эта модель объясняет широко распространенные в различных
экосистемах «волны жизни», т. е. периодические колебания численности различных
видов животных.
Однако расчеты показывают, что в системе «хищник — жертва» возможен и другой
режим, при котором наблюдается очень быстрое уменьшение численности и полное
вымирание жертвы и следующее за ним вымирание хищника (рис. 2). Такой режим
наблюдается при большой величине коэффициента у1 характеризующего смертность
жертвы за счет ее поедания хищником, и большой величине коэффициента y2, характеризующего
размножение хищника. В этой ситуации быстрое уничтожение жертвы хищником приводит
к резкому и необратимому падению численности жертвы и последующему вымиранию
хищника из-за отсутствия источника питания.
Компьютерный анализ показывает, что возможен также и ряд других динамических
режимов в этой простой экологической системе. Их исследованию и выявлению
может способствовать самостоятельное решение ряда перечисленных ниже задач
на основе программы.
Решите задачи.
Задача 1. Проверьте, как меняется амплитуда и период колебаний численности
хищника и жертвы при увеличении и уменьшении значений отдельных параметров
модели по сравнению с величинами, представленными на рисунке 1.
Задача 2. Проверьте, как меняется скорость вымирания хищника и жертвы
при изменениях значений отдельных параметров модели по сравнению с величинами,
представленными на рисунке 10.
Задача 3. Исследуйте динамику системы «хищник — жертва» при следующих
значениях параметров, указанных в скобках:
1) число зайцев в начальный момент времени (100);
2) число лисиц в начальный момент времени (38);
3) коэффициент размножения для зайцев (3);
4) коэффициент истребления для зайцев (0,03);
5) коэффициент ресурсный для зайцев (0,01);
6) коэффициент размножения для лисиц (0,05);
7) коэффициент смертности для лисиц (0,3);
8) коэффициент ресурсный для лисиц (0,001);
9) время счета (38);
Выясните, чем качественно отличается поведение экосистемы, наблюдающееся при
этих значениях параметров, от поведения, изображенном на рисунках 9 и 10
Задача 4. Исследуйте динамику системы «хищник — жертва» при следующих
значениях параметров, указанных в скобках:
1) число зайцев в начальный момент времени (100);
2) число лисиц в начальный момент времени (38);
3) коэффициент размножения для зайцев (2);
4) коэффициент истребления для зайцев (0,02);
5) коэффициент ресурсный для зайцев (0,01);
6) коэффициент размножения для лисиц (0,01);
7) коэффициент смертности для лисиц (0,3);
8) коэффициент ресурсный для лисиц (0,02);
9)время счета (38);
Выясните, чем качественно отличается поведение экосистемы, наблюдающееся при
этих значениях параметров, от поведения, изображенного на рисунках 1 и 2.
Для ввода данных нажмите Хищник-Жертва.
Закономености межвидовой конкуренции
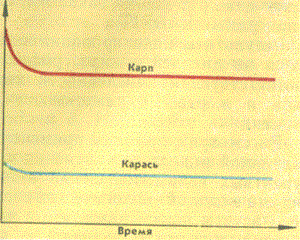 |
Рис. 3. Режим сосуществования видов в пределах одной экологической
ниши:
|
 |
Рис. 4. Режим вытеснения одного вида друг в пределах одной
экологической ниши: начальное число карпов Х0=100; начальное число карасей YO—100; коэффициент размножения карпов e1 = 0,8; коэффициент конкуренции карпов; у 1 — 0,02; коэффициент ресурсный для карпов m1 = 0,01; коэффициент размножения карасей e2=0,7; коэффициент конкуренции карасей у2=0,02; коэффициент ресурсный для карасей m2=0,01; время счета Т=15; |
Рассмотрим примеры применения указанной модели для изучения конкурентных
взаимоотношений между видами в единой экологической системе. Расчеты показывают,
что в этой системе может реализоваться ряд качественно различных режимов.
На рисунке 3 показан режим сосуществования видов в пределах одной экологической
ниши. Можно видеть, что начиная с определенного момента в экосистеме устанавливаются
постоянные численности особей конкурирующих видов. Это наблюдается при больших
величинах ресурсных коэффициентов для каждого из видов (сопоставимых с величинами
коэффициентов конкуренции для них). В рассматриваемом случае величина ресурсного
коэффициента для карпов (m1=0,02) равна величине коэффициента конкуренции
для них (y1 = 0,02), а величина ресурсного коэффициента для карасей (m2=0,01)
равна коэффициенту конкуренции для них (у2=0,01). При большом значении ресурсного
коэффициента каждый из видов организмов испытывает большие ограничения на
свою численность. Поэтому численность каждого из видов организмов падает,
что приводит к исчезновению конкуренции между ними за единый ресурс и обеспечивает
возможность устойчивого сосуществования двух видов в пределах одной экологической
ниши.
На рисунке 4 приведен другой режим — вытеснение одного вида другим. Можно
видеть, что при начальных численностях карпов и карасей, равных 100 особям,
через определенное время в экологической нише остаются только карпы. Это обусловлено
следующими причинами. Во-первых, в данном случае ресурсные коэффициенты для
карпа и карася (m1=0,01 и (m2=0,01) в 2 раза меньше, чем коэффициенты конкуренции
(y1=0,02 и у2=0,02). Это означает, что ограничения на численность видов со
стороны ресурсных коэффициентов невелики. Напротив, влияние конкурентных взаимоотношений
в этом случае существенно больше. И в конкуренции побеждает тот вид (в данном
случае карп), который имеет более высокий коэффициент размножения. Для карасей
коэффициент размножения e1=0,07, тогда как коэффициент размножения карпа e2
= 0,05, в связи с чем именно карпы побеждают в конкуренции, вытесняя карасей
из общей экологической ниши.
Компьютерный анализ показывает, что возможен также и ряд других динамических
режимов в этой простой экологической системе. Их исследованию и выявлению
может способствовать самостоятельное решение ряда перечисленных ниже задач
на основе программы
Решите задачи.
Задача 1. Проверьте, как меняется динамика численности особей конкурирующих
видов в рассматриваемой системе при увеличении и уменьшении значений отдельных
параметров модели по сравнению с величинами, представленными на рисунке 3.
Задача 2. Проверьте, как меняется динамика численности особей
конкурирующих видов в рассматриваемой системе при увеличении и уменьшении
значений отдельных параметров модели по сравнению с величинами, представленными
на рисунке 12.
Задана 3. Исследуйте динамику численности особей конкурирующих видов
в системе при следующих значениях параметров, указанных в скобках:
1) число карпов в начальный момент времени (80);
2) число карасей в начальный момент времени (100);
3) коэффициент размножения для карпов (3);
4) коэффициент конкуренции для карпов (0,01);
5) коэффициент ресурсный для карпов (0,02);
6) коэффициент размножения для карасей (1);
7) коэффициент конкуренции для карасей (0,02);
8) коэффициент ресурсный для карасей (0,02);
9) время счета (15);
Выясните, чем качественно отличается поведение экосистемы, наблюдающееся при
этих значениях параметров, от поведения, изображенного на рисунках 3 и 4.
Для ввода данных нажмите Межвидовавя конкуренция